Bring Your Own Scores
Vathy M. Kamulete
Last Updated: 2023-02-19
Source:vignettes/diy-score.Rmd
diy-score.RmdPlease see the paper (Kamulete 2022) for details. We denote the R
package as dsos, to avoid confusion with
D-SOS, the method.
DIY
To test for adverse shift, we need two main ingredients: outlier
scores from a scoring function and a way to compute a \(p-\)value (or a Bayes factor). First, the
scoring function assigns to a potentially multivariate
observation a univariate score. Second, for \(p-\)value, we may use permutations. The
prefix pt stands for permutation test. The function
pt_refit is a wrapper for this approach, provided we supply
a user-defined scoring function. Sample splitting and out-of-bag
variants are alternatives to permutations. Both use the asymptotic null
distribution and sidestep refitting (recalibrating) the scoring function
after every permutation. As a result, they can be appreciably faster
than inference based on permutations.
In Action
Take the iris
dataset for example. The training set consists of different flower
species. We use a completely random scoring function scorer
for illustration: the outlier scores are drawn from the uniform
distribution.
set.seed(12345)
data(iris)
x_train <- iris[1:50, 1:4] # Training sample: Species == 'setosa'
x_test <- iris[51:100, 1:4] # Test sample: Species == 'versicolor'
scorer <- function(tr, te) list(train = runif(nrow(tr)), test = runif(nrow(te)))
iris_test <- pt_refit(x_train, x_test, score = scorer)
plot(iris_test)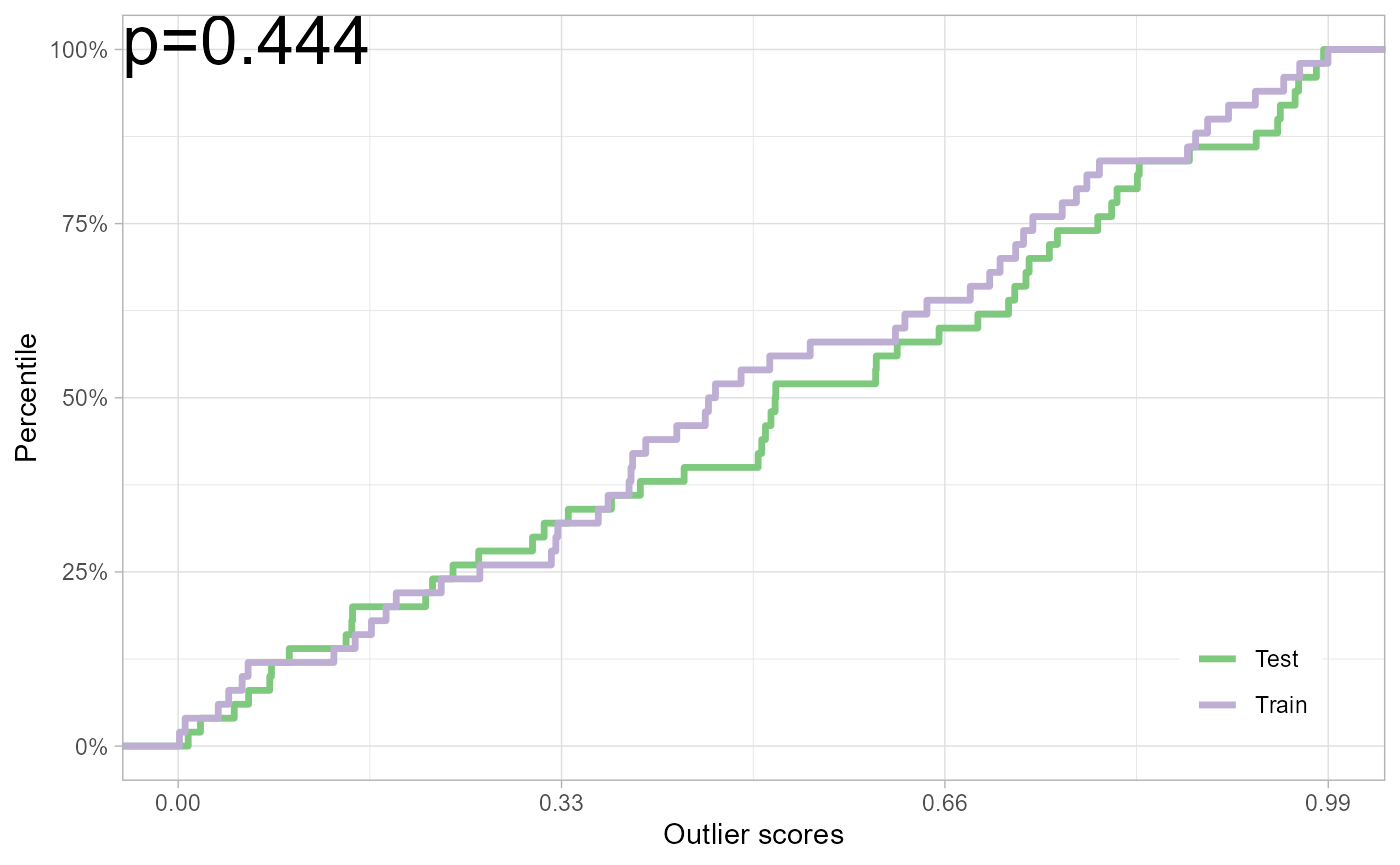
dsos provides the building blocks for plugging in your
own own scoring functions. The scorer function above is an
example of a custom scoring function. That is, you can bring your own
scores.